Cách tính đường cao trong tam giác vuông, cân, thường, đều

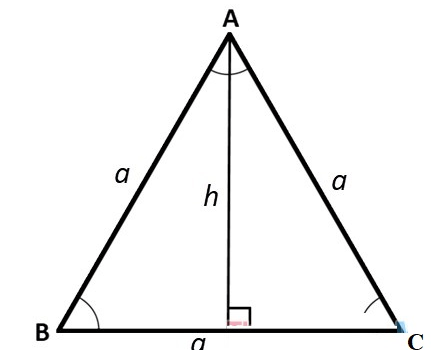
Trong bài toán toán học khi bạn cần tính đường cao trong tam giác, hãy áp dụng công thức tính đường cao trong tam giác vuông, tam giác cân, tam giác thường, tam giác đều sau để giải bài toán một cách chính xác! Cùng Tài Liệu Trọn Đời tìm hiểu nhé!

Công thức tính đường cao trong tam giác

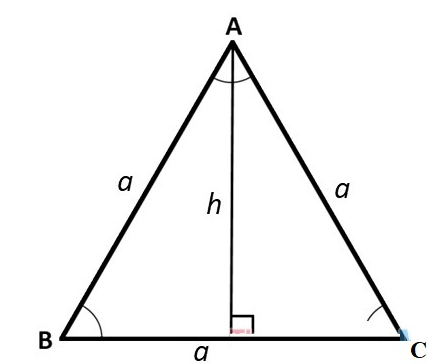
Cách tính đường cao trong tam giác thường

Tam giác thường là tam giác có ba cạnh và ba góc đều khác nhau. Công thức tính đường cao h trong tam giác thường như sau:

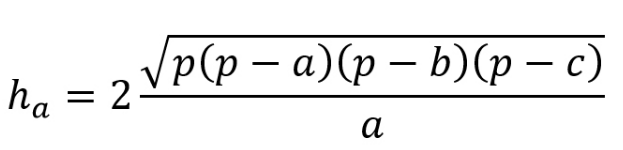
Trong đó

• a, b, c là độ dài các cạnh của tam giác
• h là chiều cao trong tam giác
• p là nửa chu vi của tam giác, p = (a + b + c) : 2

Công thức tính đường cao trong tam giác đều

Tam giác đều có ba cạnh bằng nhau, ba góc bằng nhau và mỗi góc đều bằng 60 độ. Công thức tính đường cao trong tam giác đều là:

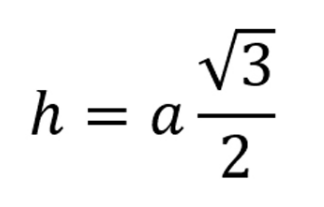
Trong đó

• h: Chiều cao của tam giác đều
• a: Độ dài cạnh của tam giác đều

Công thức tính đường cao trong tam giác vuông

Tam giác vuông có một góc vuông. Công thức tính đường cao trong tam giác vuông như sau:

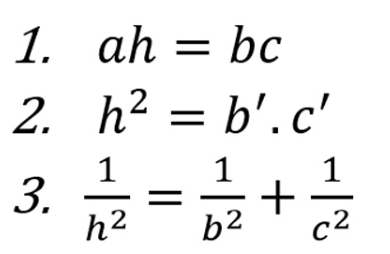
Trong đó

• a, b, c: Mỗi cạnh của tam giác vuông
• b’: Đường chiếu của cạnh b lên cạnh huyền
• c’: Đường chiếu của cạnh c lên cạnh huyền
• h: Chiều cao của tam giác vuông, là đường kẻ từ đỉnh góc vuông A vuông góc với cạnh huyền ABC

Công thức tính đường cao trong tam giác cân

Giả sử tam giác ABC cân tại A, đường cao AH vuông góc với cạnh AC như sau:

Công thức tính đường cao AH trong tam giác cân ABC là:

Vì tam giác ABC cân tại A, nên đường cao AH cũng là đường trung tuyến, nên:

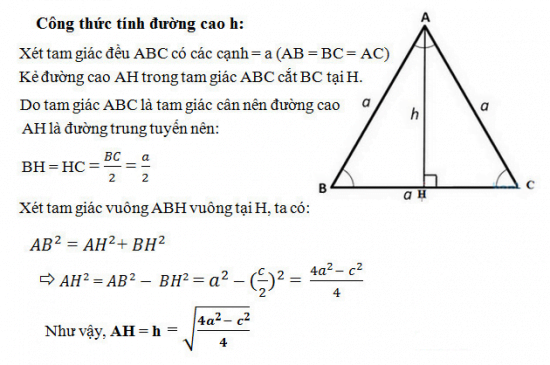
Hoặc bạn có thể sử dụng công thức Pythagoras trong tam giác vuông ABH vuông tại H:

AH² + BH² = AB²

⇒ AH² = AB² − BH²

Bài toán ví dụ

Ví dụ 1: Cho tam giác ABC, cạnh AB = 4 cm, cạnh BC = 7 cm, cạnh AC = 5 cm. Tính đường cao AH từ A xuống BC tại H và tínhDiện tích tam giác ABC.

Giải:

Nửa chu vi tam giác: P = (AB + BC + AC):2 = (4 + 7 + 5):2 = 8 cm

Ví dụ 2: Cho tam giác ABC vuông tại A, có đường cao AH, biết AB: AC = 3; AB + AC = 21cm. a. Tính độ dài mỗi cạnh của tam giác ABC. b. Tính đường cao AH.

Giải:

Đường cao AH = 7,2 cm Trên đây là toàn bộ công thức tính đường cao trong tam giác vuông, tam giác thường, tam giác cân và tam giác đều mà bạn đọc có thể học thuộc lòng để áp dụng vào các bài toán!

Nguồn tham khảo: bierelarue.com.vn