
Bất đẳng thức Cosi (Cauchy) có tên gọi chính xác là bất đẳng thức giữa trung bình cộng và trung bình nhân. Ngoài ra bất đẳng thức Cosi còn có tên gọi là bất đẳng thức AM-GM.
Chúng ta sẽ làm quen với bất đẳng thức Cosi 2 số, 3 số, 4 số lần lượt từ lớp 8 tới lớp 9, 10 vì vậy mỗi em nên nhớ công thức để áp dụng vào bài tập kiểm tra trên lớp.
Bất đẳng thức Cosi

Bất đẳng thức Cosi là khái niệm dùng để chỉ bất đẳng thức so sánh giữa trung bình cộng và trung bình nhân của n số thực không âm.
Trong đó, trung bình cộng của n số thực không âm luôn lớn hơn hoặc bằng trung bình nhân của chúng. Trung bình cộng chỉ bằng trung bình nhân khi và chỉ khi n số đó bằng nhau.
Bất đẳng thức Cosi 2 số không âm
Dấu = xảy ra khi và chỉ khi a = b.
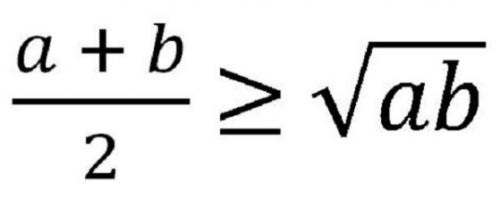
Chứng minh:
Ta thấy với a = 0 hoặc b = 0 thì bất đẳng thức luôn đúng. Vì vậy, bạn đọc chỉ cần chứng minh bất đẳng thức Cosi với 2 số dương.
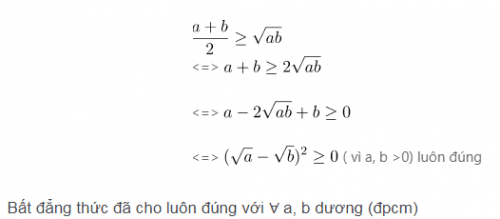
Bất đẳng thức Cosi 3 số không âm
Dấu = xảy ra khi và chỉ khi a = b = c.
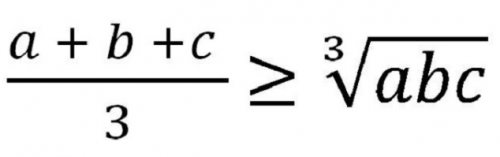
Chứng minh : Với a = 0 hoặc b = 0 hoặc c = 0 thì bất đẳng thức luôn đúng. Vì vậy, bạn đọc chỉ cần chứng minh bất đẳng thức Cosi với 3 số dương.
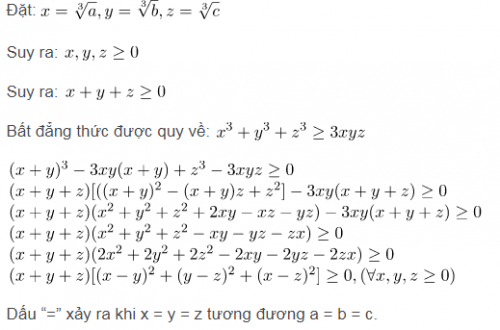
Bất đẳng thức Cosi 4 số không âm
Dấu = xảy ra khi và chỉ khi a = b = c = d.
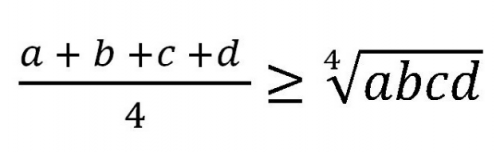
Chứng minh : Với a = 0 hoặc b = 0 hoặc c = 0 hoặc d = 0 thì bất đẳng thức luôn đúng. Vì vậy bạn đọc chỉ cần chứng minh bất đẳng thức Cosi với 4 số dương.
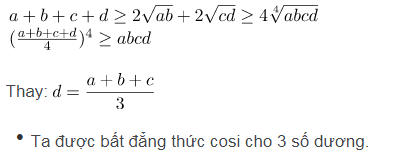
Bất đẳng thức Cosi n số không âm
Với x1, x2,…, xn là n số thực không âm
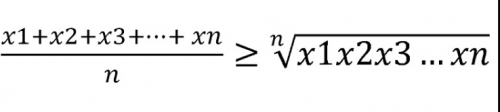
Bản chất : Khi n=2, bất đẳng thức là đúng. Nếu bất đẳng thức đúng với n số, thì cũng đúng với 2n số.
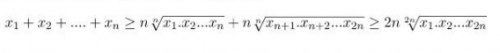
Theo nguyên lý quy nạp, nếu bất đẳng thức đúng với n được coi là mũ của 2. Một cách tương tự, nếu bất đẳng thức đúng với n số, ta cũng chứng minh được rằng nó cũng đúng với n – 1 số như sau:
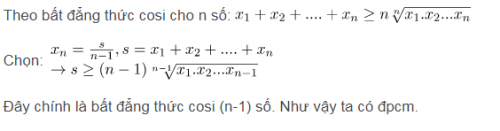
Tổng kết
Từ bài viết trên, chúng ta có thể hiểu được một cách cơ bản về các công thức bất đẳng thức cosi và đã chứng minh chúng một cách toàn diện để áp dụng vào các bài tập và câu hỏi trắc nghiệm từ lớp 8 đến lớp 10!
Nguồn tham khảo: bierelarue.com.vn


