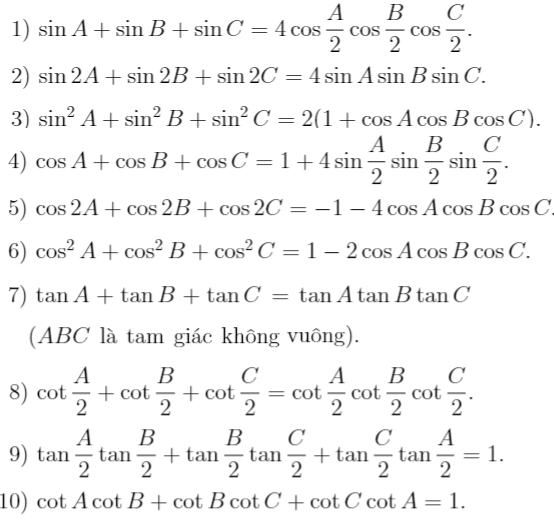Công thức lượng giác rất phổ biến trong mỗi kỳ thi trung học phổ thông, cũng như là trong mỗi kỳ thi đại học. Chính vì thế việc thuộc lòng công thức lượng giác là rất quan trọng khi bạn chuẩn bị cho các kỳ thi này.
Dưới đây là một số công thức lượng giác từ cơ bản đến nâng cao và cách thuộc lòng chúng một cách hiệu quả.
Bảng công thức lượng giác Sin Cos

Bảng công thức lượng giác và các cung liên quan đặc biệt
Giá trị lượng giác của một góc không đổi
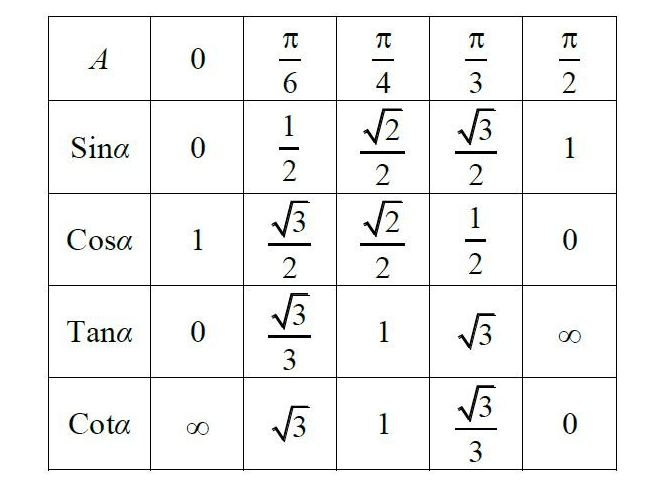
Hãy nhớ bảng cung liên kết: cos đối, sin bù, phụ chéo
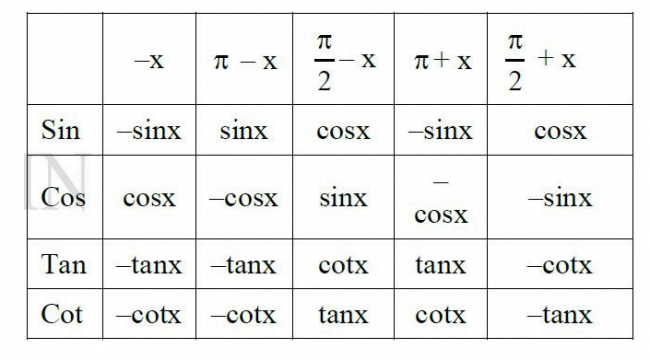
Các cung liên quan đặc biệt


Lưu ý: Hãy nhớ bảng công thức sau: cos đối, sin bù, phụ chéo, hơn, kém π, tan, cos
Công thức lượng giác cơ bản

Công thức nhân đôi, nhân 3, công thức hạ bậc

Công thức cộng
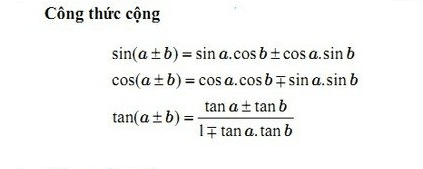
Cách biến tổng thành tích

Phương pháp biến đổi tích thành tổng

Công thức lượng giác được tối ưu hóa
Biến đổi hằng đẳng thức trong công thức lượng giác
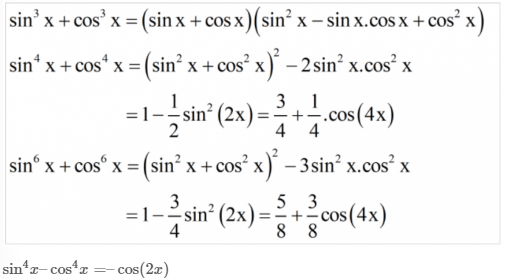
Công thức liên quan đến tổng và hiệu giữa các giá trị lượng giác
- Mối quan hệ giữa sin và cos
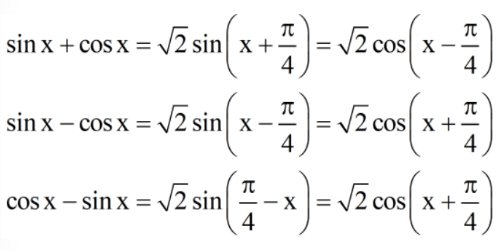
- Mối quan hệ giữa tan và cot
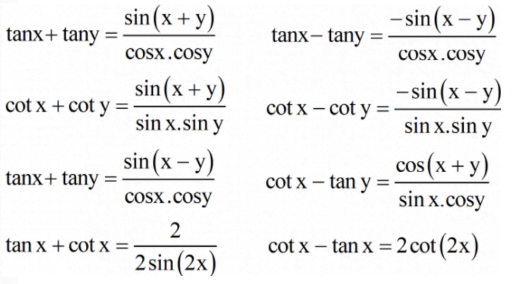
Các phương trình cơ bản về lượng giác trong tam giác
- Giả sử tam giác ΔABC với các đỉnh A, B, C. Liên kết giữa các góc trong tam giác này

- Công thức chia góc thành hai phần bằng nhau
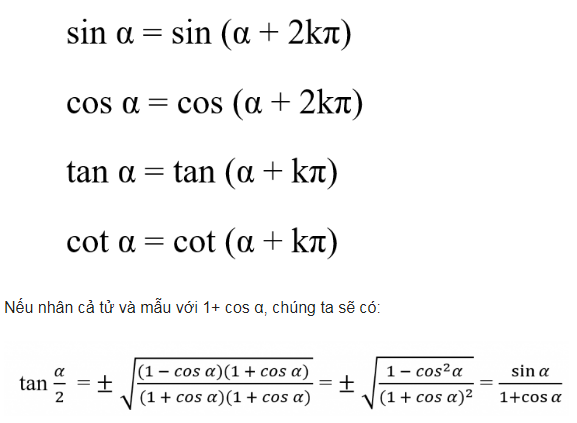

Cách nhanh nhất để học thuộc các công thức lượng giác
Việc học thuộc các công thức lượng giác là điều quan trọng nhưng cũng gặp khó khăn. Dưới đây là một số cách mà mỗi giáo viên đã nghĩ ra để giúp học sinh nhanh chóng thuộc lòng bảng công thức lượng giác:
Bài thơ về công thức cộng lượng giác
Cos + cos = 2 cos cos
cos trừ cos = trừ 2 sin sin
Sin + sin = 2 sin cos
sin trừ sin = 2 cos sin.
Sin thì sin cos cos sin
Cos thì cos cos sin sin “coi chừng” (dấu trừ).
Tang tổng thì lấy tổng tang
Chia một trừ với tích tang.
Cách học giá trị lượng giác cung đặc biệt
- Cos đối, sin bù, phụ chéo, khác pi tan
- Cosin của 2 góc đối bằng nhau; sin của 2 góc bù nhau thì bằng nhau; phụ chéo là 2 góc phụ nhau thì sin góc này = cos góc kia, tan góc này = cot góc kia; tan của 2 góc hơn kém pi thì bằng nhau.
Cách học công thức lượng giác nhân ba
Nhân ba một góc bất kỳ,
sin thì ba bốn, cos thì bốn ba,
dấu trừ đặt giữa 2 ta, lập phương chỗ bốn.
Công thức gấp đôi
+Sin gấp đôi = 2 sin cos
+Cos gấp đôi = bình cos trừ bình sin
= trừ 1 + 2 lần bình cos
= + 1 trừ 2 lần bình sin
+Tang gấp đôi
Tang đôi ta lấy đôi tang (2 tang)
Chia 1 trừ lại bình tang, ra ngay tức thì.Cách nhớ công thức: tan(a+b)=(tan+tanb)/1-tana.tanb
tan một tổng 2 tầng cao rộng
trên thượng tầng tan + tan tan
dưới hạ tầng số 1 ngang tàng
dám trừ một tích tan tan oai hùng
Cách học biến đổi tổng thành tích của các công thức lượng giác một cách nhanh nhất
sin tổng lập tổng sin cô
cô tổng lập hiệu đôi cô đôi chàng
còn tan tử + đôi tan (hoặc là: tan tổng lập tổng 2 tan)
một trừ tan tích mẫu mang thương sầu
gặp hiệu ta chớ lo âu,
đổi trừ thành + ghi sâu vào lòng
Cách nhớ biến đổi tích thành tổng của công thức lượng giác một cách dễ dàng nhất
Cos cos nửa cos-+, + cos-trừ
Sin sin nửa cos-trừ trừ cos-+
Sin cos nửa sin-+ + sin-trừ.
Kết luận
Trên đây là một tổng hợp đầy đủ công thức lượng giác cơ bản và tối ưu hóa dành cho học sinh lớp 10 và 11, để học sinh có thể thuộc lòng và nhanh chóng áp dụng khi giải bài tập lượng giác.
Nguồn tham khảo: bierelarue.com.vn